Зірчастий октаедр

Зірчастий октаедр
Граней	8 правильних трикутників
Ребер	12
Вершин	8
Символ Шлефлі	$3$
Діаграма Коксетера	∪ =
Група симетрії	октаедральна (Oh) [4,3] або [[3,3]]
Дуальний многогранник	самодвоїстий

Зірчастий октаедр або stella octangula — єдина зірчаста форма октаедра. Латинську назву stella octangula многограннику дав 1609 року Кеплер, хоча тіло було відоме й ранішим геометрам. Так, його зображено у праці Пачолі De Divina Proportione 1509 року.

Многогранник є найпростішим із п'яти правильних з'єднань многогранників.

Зірчастий октаедр можна розглядати як тривимірне узагальнення гексаграми — гексаграма є двовимірною фігурою, утвореною двома накладеними один на одного правильними трикутниками, центрально симетричними один одному, і так само зірчастий октаедр можна утворити з двох центрально симетричних тетраедрів, що перетинаються. Його ж можна розглядати як одну зі стадій побудови тривимірної сніжинки Коха, фрактального тіла, що будується повторюваним приєднанням менших тетраедрів до кожної трикутної поверхні більшого тіла. Початковою стадією побудови сніжинки Коха є один центральний тетраедр, а другою стадією, отриманою додаванням чотирьох менших тетраедрів до граней центрального тетраедра, буде зірчастий октаедр.

Побудова

Зірчастий октаедр можна отримати кількома шляхами:

• Це ззірчення правильного октаедра, що зберігає його площини граней. Грані зірки дуже прості: (Див. модель Веннінджера W₁₉).
• Він є правильним з'єднанням многогранників — двох тетраедрів (тетраедра і двоїстого йому тетраедра).
• Його можна отримати доповненням правильного октаедра трикутними пірамідами до кожної грані. У цій побудові многогранник має ту ж топологію, що й опукле каталанове тіло триакісоктаедр, яке має значно коротші піраміди.
• Це огранування куба зі збереженням вершин.

Пов'язані концепції

У поданого у вигляді сферичної мозаїки зірчастого октаедра ребра у з'єднанні двох тетраедрів утворюють ромбододекаедр

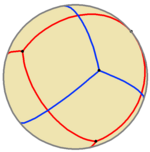
Можна побудувати з'єднання двох сферичних тетраедрів, як показано на малюнку.

Два тетраедри у з'єднанні зоряного октаедра є «десмічними», що означає (якщо розглядати їх як прямі в проєктивному просторі), що кожне ребро одного тетраедра перетинає протилежне ребро іншого тетраедра. Один із таких перетинів видно в зірчастому октаедрі. Інший перетин виявляється в нескінченній точці проєктивної площини між двома паралельними ребрами двох тетраедрів. Ці два тетраедри можна доповнити до десмічної системи трьох тетраедрів, де вершинами третього тетраедра є три точки перетину на нескінченності і центроїд двох скінченних тетраедрів. Також дванадцять вершин тетраедрів утворюють точки конфігурації Реє.

124 магнітні кулі, розташовані у формі зірчастого октаедра

Числа зірчастого октаедра — фігурні числа, що підраховують число куль, які можна розташувати всередині зірчастого октаедра. Ці числа рівні

0, 1, 14, 51, 12, 51, 124, 245, 426, 679, 1016, 1449, 1990, … (послідовність A007588 з Онлайн енциклопедії послідовностей цілих чисел, OEIS)

У популярній культурі

Зірчастий октаедр разом із деякими іншими многогранниками і з'єднаннями многогранниками зображено на картинах Ешера «Зірки» та «Подвійний астероїд» (1949).

Галерея

• 
  Повне симетричне огранування куба.
• 
• 
• 
• 
• 
• 
• 

Література

• P. Cromwell. Polyhedra Polyhedra. — United Kingdom : Cambridge University Press, 1997. — С. 79–86 Archimedean solids. — ISBN 0-521-55432-2.
• H.S.M Coxeter. 3.6 The five regular compounds, pp.47-50, 6.2 Stellating the Platonic solids, pp.96-104 // Regular Polytopes. — 3rd edition. — New York : Dover Publications Inc, 1973. — ISBN 0-486-61480-8.
• George W. Hart. The Polyhedra of M.C. Escher // WEB-статья. — 1996.
• H. S. M. Coxeter. A special book review: M. C. Escher: His life and complete graphic work // The Mathematical Intelligencer. — 1985. — Т. 7, вип. 1. — DOI:10.1007/BF03023010.

Посилання

• VRML модель: [1]
• Weisstein, Eric W. Зірчастий октаедр(англ.) на сайті Wolfram MathWorld.
• KlitzingPolytopes|.. /incmats/so.htm Richard Klitzing, 3D compound Архівовано листопад 6, 2015 на сайті Wayback Machine.